探索拓扑结构的多种类型及应用领域（拓扑结构的分类与实际应用领域的研究进展）

在现代科学和工程领域中，拓扑结构是一种重要的概念，它描述了事物之间的连接方式和相互关系。不同类型的拓扑结构在各个应用领域都有广泛的应用。本文将探索拓扑结构的多种类型及其在实际应用领域中的研究进展。

一：欧拉特性与欧拉图的应用

欧拉特性是指拓扑结构中的点、边和面之间的关系，而欧拉图是具有特定欧拉特性的图形。欧拉图在网络通信、电路设计和地理学等领域有广泛应用。

二：连通性与连通图的应用

连通性描述了拓扑结构中各元素之间是否具有连通性，而连通图是指所有节点之间都存在路径的图形。连通图在社交网络分析、物流规划和电力系统设计等领域有着重要的应用。

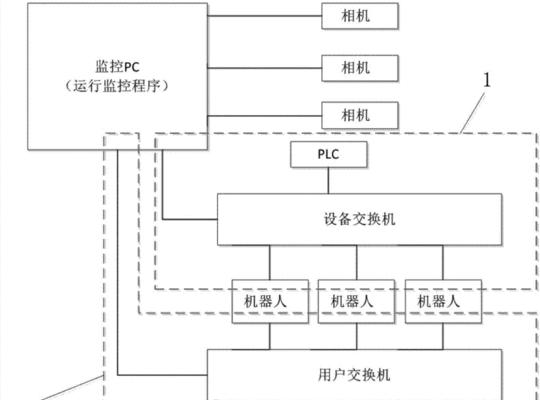
三：完备性与完全图的应用

完备性描述了拓扑结构中的每个节点是否与其他节点直接相连，而完全图是指每个节点都与其他节点直接相连的图形。完全图在密码学、计算机网络和社交网络中的信息传递等方面有重要作用。

四：环的存在与环图的应用

环是指拓扑结构中形成闭合路径的元素，而环图是具有环结构的图形。环图在电路设计、交通规划和化学结构分析等领域有广泛的应用。

五：树状结构与树图的应用

树状结构是一种无环且连通的拓扑结构，而树图是具有树状结构的图形。树图在数据结构、分类学和组织管理等领域有着重要的应用。

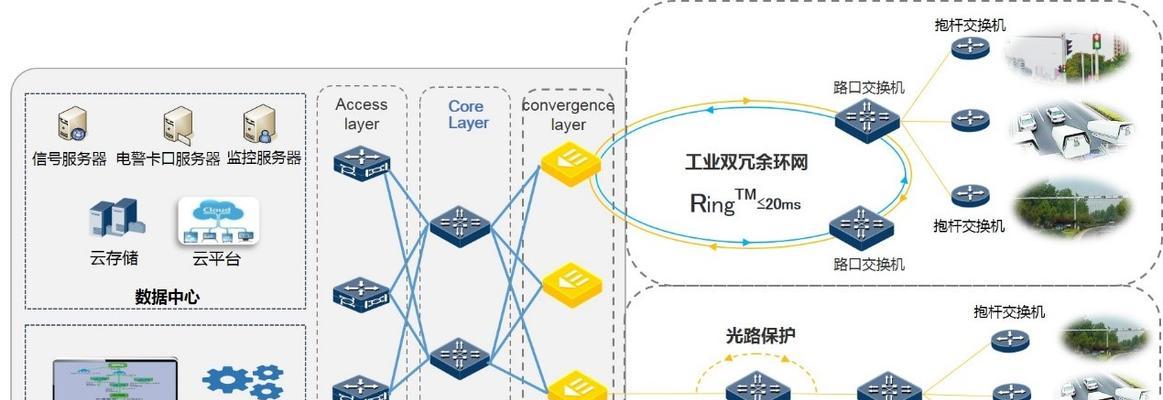
六：网格结构与网格图的应用

网格结构是由水平线和垂直线组成的规则网状结构，而网格图是具有网格结构的图形。网格图在计算机图形学、城市规划和遥感影像处理等领域有广泛的应用。

七：超立方体结构与超立方图的应用

超立方体结构是由一系列正方体通过共享顶点或边连接而成的结构，而超立方图是具有超立方体结构的图形。超立方图在计算机网络、并行计算和量子计算等领域有着重要的应用。

八：流形结构与流形图的应用

流形结构描述了拓扑空间中局部与整体之间的关系，而流形图是具有流形结构的图形。流形图在数据挖掘、人工智能和信号处理等领域有广泛的应用。

九：复杂网络结构与复杂网络图的应用

复杂网络结构是由大量节点和连接组成的非规则拓扑结构，而复杂网络图是具有复杂网络结构的图形。复杂网络图在社交网络分析、脑神经网络研究和互联网拓扑分析等方面有重要作用。

十：应用领域之一：信息通信网络

拓扑结构在信息通信网络中起着至关重要的作用，不同的拓扑结构可以决定网络的传输性能、容错性和可扩展性。星型拓扑在局域网和广域网中常用，而环型拓扑在光纤环网中被广泛应用。

十一：应用领域之二：物流与交通规划

拓扑结构在物流和交通规划领域中的应用可以帮助优化物流路径、交通流量和运输成本。连通图可以用于规划最短路径和优化交通信号控制，网格图可以用于城市道路规划和交通拥堵分析。

十二：应用领域之三：生物学与生态学

拓扑结构在生物学和生态学领域中的应用可以帮助理解生物群落之间的相互关系和能量传递路径。食物链和食物网的拓扑结构可以用来研究生态系统稳定性和物种多样性。

十三：应用领域之四：社会网络分析

拓扑结构在社会网络分析中起着重要作用，可以揭示人际关系、信息传播和社区发现等问题。复杂网络图可以用来研究社交媒体中的信息传播路径和社区结构。

十四：应用领域之五：能源与电力系统

拓扑结构在能源和电力系统领域中的应用可以优化能源传输、电力供应和电网稳定性。树状结构和环型结构可以用于电力系统的供电和配电，超立方图可以用于分布式能源系统的优化。

十五：

拓扑结构是一种重要的概念，不同类型的拓扑结构在各个应用领域都有广泛的应用。通过研究拓扑结构的多种类型和应用领域，可以帮助我们更好地理解和优化现实世界中的各种系统和网络。